Fractals (Awaiting copyright permissions on some images)

Fractals : are processes or images that exhibit something called self-similarity.  For example something that is made up a reduced version of itself.

The picture below shows how the fern is made up of a range of tiny ferns.  Each leaf of the fern is in fact a smaller version of the entire fern.  The whole fern is simply made up of reduced versions of itself.  Every leaf which branches from the fern is an even smaller one and this form of self-similarity continues forever.  A fractal fern contains many repeated portions of different sizes.  

In nature many objects exhibit self-similarity for example landscapes.  The study of this phenomena has been around for over 100 years and initially introduced via journals and mathematical literature.  Like so many revolutionary ideas they were denounced. One famous mathematician called Charles Hermite even referred to them as 'monsters'.

Benoit B. Mandelbrot, who is often called the 'father of fractals', investigated the relationship between fractals and nature. He showed that many fractals existed in nature and could accurately model some phenomenon. 

"As he researched, he and his collaborators introduced many new types of fractals to model more complex things like trees or mountains. He furthered the idea of fractional dimension and later coined the term 'fractals' from this revolutionary concept".

Some properties of fractals include, self-similarity, or the repetition of patterns at all scales. Another property that commonly exists in fractals is infinite complexity and detail.

The complexity and properties of fractals means that they can be used in a number of real-world applications.  Fractals can be used for modeling things in areas as diverse as: biology, geography, economics and medicine.

In biology both plants and animals exhibit properties of self-similarity as has already been seen in the case of the fern.  In humans branches of arteries and veins can be modeled using fractals, as well as a number of other things including:  kidney structure, skeletal structure, heart and brain waves and the nervous system.

In some instances the stock market and economic meters can exhibit properties of self-similarity and as such fractals can be used here.

Fractals are also used in the world of fine art where they are used to accurately model music produced by a wide variety of composers.  They can also be used to create beautiful "paintings" of landscapes and attractive pictures, examples of which can be found bellow.

In the film Apollo 13, a picture of the moon was generated using fractals, they were particularly useful because no matter how far is zoomed, the detail of an object can be preserved.

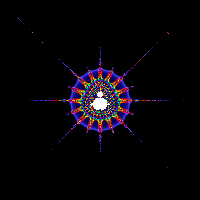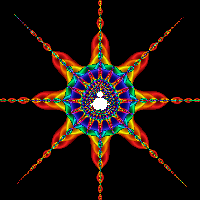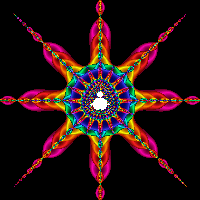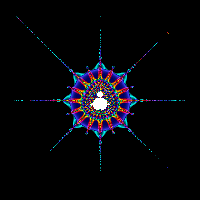
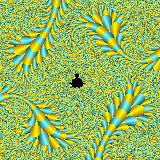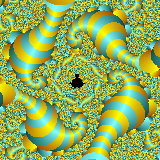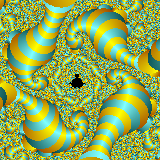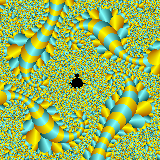
Please see below some examples of fractals.  Fractals are both an unusual and beautiful phenomenon and for more information about this fascinating topic please visit the links below.  Please note that the following pictures may not be reproduced without prior permission from Fantastic Fractals Online! and Mind-Boggling Fractals websites.


Sierpenski's Triangle (Image courtesy of Fantastic Fractals Online!)


Sierpenski's Gasket (Image courtesy of Fantastic Fractals Online!)


Koch Curve (Image courtesy of Fantastic Fractals Online!)


Koch Curve (Image courtesy of Fantastic Fractals Online!)

Source: Information, extracts and inspiration for this article courtesy of the Fantastic Fractals Online! website.

Examples of fractals as an interesting art form all of the images below are courtesy of Mind-Boggling Fractals website.